Programando una red neuronal simple
El día de hoy toca hablar de redes neuronales. Las redes neuronales han estado empujando el horizonte de lo que se creía posible en la inteligencia artificial, y casi cada semana hay noticias nuevas de un sistema inteligente basado en redes neuronales. Hoy vamos a programar una red neuronal muuuy sencilla.
El Perceptrón
Uno de los primeros modelos artificiales de una neurona fue inventado en 1957 por Frank Rosenblatt, un profesor de psicología en la Universidad de Cornell. Rosenblatt diseñó un algoritmo de clasificación con aprendizaje supervisado, es decir, un algoritmo que aprende a clasificar nuevos datos basado en datos conocidos.
Un perceptrón es un modelo con varias entradas, que su vez son ponderadas, tiene un término independiente y una salida binaria que depende de si la suma ponderada de las entradas es mayor o menor a cero. En la figura 1 podemos ver cómo se calcula la salida de un perceptrón simple.
 </img>
</img>Figura 1. Ecuación de la salida del perceptrón.
El producto punto entre el vector w y las entradas x es el promedio ponderado de las entradas. Una visualización de nuestro perceptrón sería la siguiente:
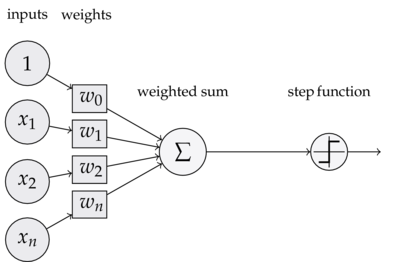 </img>
</img>Figura 2. Un perceptrón simple con 3 entradas ponderadas, un término independiente (observa los parámetros w) y una salida.
En la figura 2, nuestro término independiente es el parámetro w0. De esta manera, podemos reducir la salida a un producto punto entre dos vectores.
Datos
Las entradas del perceptrón pueden ser números que cuantifiquen cualquier cosa. Por ejemplo, podemos hacer un modelo para clasificar hombres y mujeres según su peso y su estatura*. Los siguientes datos obtuve de amigos míos:
| Estatura . | Peso . | Género . |
|---|---|---|
| 170 | 56 | Mujer(1) |
| 172 | 63 | Hombre(0) |
| 160 | 50 | Mujer(1) |
| 170 | 63 | Hombre(0) |
| 174 | 66 | Hombre(0) |
| 158 | 55 | Mujer(1) |
| 183 | 80 | Hombre(0) |
| 182 | 70 | Hombre(0) |
| 165 | 54 | Mujer(1) |
Implementando el perceptron
Para la implementación, vamos a crear una clase Perceptron, que va a encapsular toda la funcionalidad. Vamos a hacerlo en python para que cualquiera pueda probarlo en sus propias máquinas. Primero ponemos el constructor:
import random
class Perceptron:
def __init__(self,input_number,step_size=0.1):
self._ins = input_number # Número de parámetros de entrada
# Seleccionamos pesos aleatorios
self._w = [random.random() for _ in range(input_number)]
self._eta = step_size # La tasa de convergencia
...La variable self._w son los pesos w, la variable self._ins es el número de variables de entrada, etc.
Ahora necesitamos también la función para calcular la salida del perceptron. Como sabemos, sólo es necesario calcular un producto punto entre la entrada y los pesos, y verificar si es mayor a cero o no:
class Perceptron:
...
def predict(self,inputs):
# Producto punto de entrada y pesos
weighted_average = sum(w*elm for w,elm in zip(self._w,inputs))
if weighted_average > 0:
return 1
return 0
...No se confundan con la línea del producto punto. No es más que un truco de Python llamado comprensión de lista. Vale la pena que lo aprendan ; )
El último elemento que necesitamos es la función de entrenamiento del perceptron. Antes de agregarla, volvamos a la figura 1, con la ecuación de la salida. Y pensemos en qué ocurre cuando hay errores.
Si tenemos una mujer (la salida correcta sería 1), y el modelo incorrectamente da una salida de 0, entonces tendríamos que reducir los pesos, para que no se vuelva a equivocar. En el caso contrario, deberíamos incrementar los pesos para evitar el error. Pues de hecho, así es como funciona el algoritmo de aprendizaje del perceptron (y tiene sustento matemático, del que hablaremos posteriormente, pero por lo pronto, conformémonos).
class Perceptron:
...
def train(self,inputs,ex_output):
output = self.predict(inputs)
error = ex_output - output
# El error es la diferencia entre la salida correcta y la esperada
if error != 0:
self._w = [w+self._eta*error*x for w,x in
zip(self._w,inputs)]
return errorLa variable self._eta se llama así por la letra griega, y es una tasa de convergencia. Un parámetro comunmente utilizado en análisis numérico para suavizar la convergencia de un algoritmo.
Y con eso tenemos el código de nuestra clase perceptron listo. Con esto podemos agregar código para probarlo y verlo funcionando. El código para probarlo es el siguiente:
#!/usr/bin/env python
from perceptron import Perceptron
## Datos de hombres y mujeres
input_data = [[1.7,56,1], # Mujer de 1.70m y 56kg
[1.72,63,0],# Hombre de 1.72m y 63kg
[1.6,50,1], # Mujer de 1.60m y 50kg
[1.7,63,0], # Hombre de 1.70m y 63kg
[1.74,66,0],# Hombre de 1.74m y 66kg
[1.58,55,1],# Mujer de 1.58m y 55kg
[1.83,80,0],# Hombre de 1.83m y 80kg
[1.82,70,0],# Hombre de 1.82m y 70kg
[1.65,54,1]]# Mujer de 1.65m y 54kg
## Creamos el perceptron
pr = Perceptron(3) # Perceptron con 3 entradas
## Fase de entrenamiento
for _ in range(100):
# Vamos a entrenarlo varias veces sobre los mismos datos
# para que los 'pesos' converjan
for person in input_data:
output = person[-1]
inp = [1] + person[0:-1] # Agregamos un uno por default
err = pr.train(inp,output)
h = float(raw_input("Introduce tu estatura en centimetros.- "))
w = float(raw_input("Introduce tu peso en kilogramos.- "))
if pr.predict([1,h,2]) == 1: print "Mujer"
else: print "Hombre"Como ven, tenemos que iterar varias veces para lograr que el algoritmo converja. En la Figura 3 se puede ver cómo ocurrieron errores en el resultado, y cómo tras algunas iteraciones de entrenamiento dejó de haber errores.
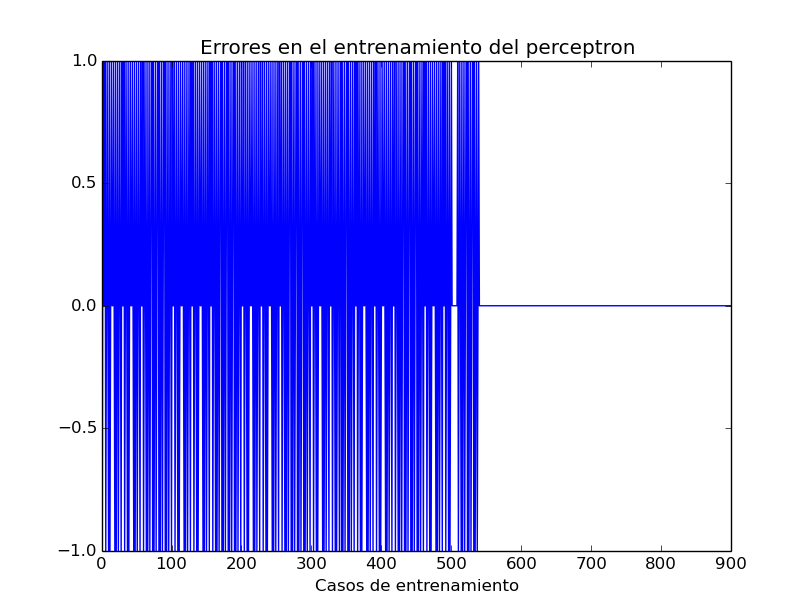 </img>
</img>
Figura 3. Variabilidad del error en entrenamiento de perceptron.
Y para concluir, en la figura 4 pueden ver cómo la frontera entre hombres y mujeres quedó tras el entrenamiento. Como ven, nuestro perceptrón logró clasificar nuestros datos, pero tal vez no le vaya tan bien con datos diferentes.
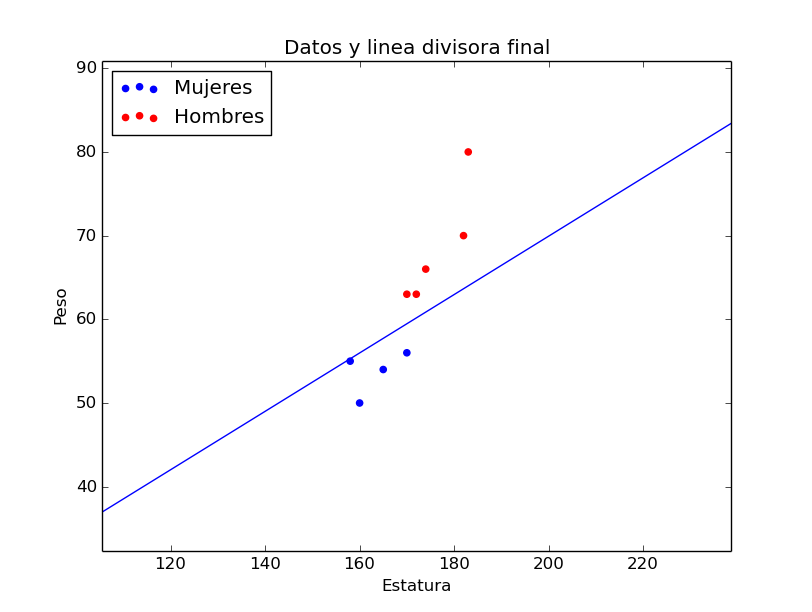 </img>
</img>
Figura 4. Datos conocidos y frontera obtenida tras el entrenamiento..
- Vale la pena mencionar también que clasificar perfectamente a hombres y mujeres por peso y estatura no es posible, pero con este algoritmo podemos obtener una predicción más o menos razonable.
Para concluir
Hemos implementado un pequeño Perceptrón. Uno de los algorítmos de aprendizaje más sencillos que existen, y un ejemplo básico de red neuronal. Pueden descargar el código en zip, o con git y correrlo en sus propias máquinas - se los recomiendo ; ).
Posteriormente escribiré un post nuevo donde vamos a estudiar (de manera sencilla) las matemáticas del perceptrón, y los avances de las redes neuronales, y en particular de las redes neuronales profundas.
Comentarios bienvenidos y gracias por compartir! ;)
