Hace un poco más de dos meses, el mundo de los algoritmos fue sacudido con un nuevo resultado en Isomorfismo de Grafos. El profesor Lázló Babai de la Universidad de Chicago es un brillante académico de ciencia de la computación y matemáticas. De origen Húngaro, el profesor Lázló realiza investigación en la Teoría de la Complejidad, matemáticas discretas y algoritmos. Hace un par de meses, el profesor Lázló (conocido entre sus amigos como Laci) anunció que había descubierto un algoritmo cuasi-polinomial que permite resolver el el problema de Isomorfismo de Grafos. Vamos a ver qué significa todo esto…

Nota: Antes de continuar, es importante que tengan una idea de qué es la Notación Big O, dado que vamos a hablar mucho sobre complejidad de algoritmos.

##¿El iso- qué de Grafos? Isomorfismo de Grafos es un concepto de la Teoría de Grafos. Dados dos grafos, queremos saber si esos dos grafos son isomórficos - o sea, si en realidad representan la misma “estructura”. Por ejemplo, en la Figura 1 podemos ver dos grafos ordenados de distinta forma, pero si observamos de cerca, podemos ver que su estructura es la misma.

</img></img>
Figura 1. Grafo A y Grafo B. Estos dos grafos son isomórficos.

¿Se nota? Observen que el nodo Azul está conectado con los nodos Naranja, Rojo y Verde en ambos grafos; luego, el nodo Morado está conectado con los nodos Amarillo, Rosa y Azul claro - también en ambos grafos. Observen que con todos los nodos, el resultado es siempre el mismo. Tómense un minuto para ver que es cierto. Entonces, buscamos un algoritmo eficiente que recibe dos grafos, y puede determinar si son isomórficos o no.

Isomorfismo de Grafos es un problema interesante, entre otras razones, porque es uno de pocos problemas que no se sabe bien si son del gripo de problemas P, o si es NP-Completo (más sobre esto adelante). Esto significa que -hasta no verificar que el Profesor Lázsló esté en lo correctio- no se sabe muy bien si el Isomorfismo de Grafos es un problema ‘fácil’ de resolver, o si es bastante ‘difícil’ de resolver. De hecho, la cuestión de si el Isomorfismo de Grafos puede ser resuelto en tiempo polinomial ha sido un problema abierto por más de cuarenta años!

P y NP

Esta sección es un poquito pesada. Si no quieres leer sobre la Teoría de la Complejidad, puedes saltártela - pero es interesante y muy importante. ;)

El problema de P vs NP es uno de los problemas más importantes de la ciencia de la computación, y de las matemáticas modernas. De hecho, es uno de los 10 Problemas del Milenio; y es un área con muchísimos esfuerzos de investigación en todo el mundo. Es casi como un esfuerzo cartográfico, para construir un mapa de la complejidad de los distintos problemas algorítmicos.

P y NP son dos clases de problemas algorítmicos. Por un lado, P es la clase de problemas que pueden ser resueltos en tiempo polinomial en función del tamaño de la entrada en una Máquina Determinística de Turing; mientras que NP es la clase de problemas que pueden ser verificados por una máquina determinística de Turing. Esto suena muy técnico, pero no se asusten. Una máquina de Turing no es más que un modelo matemático de una computadora.

En términos más simples, P es la clase de problemas que pueden ser resueltos ‘rápidamente’. Por ejemplo, ordenar una lista de N números puede hacerse en O(n log(n)). Es decir que puede hacerse en tiempo polinomial.

Por otro lado, NP es la clase de problemas que puede ser difícil de resolver, pero es fácil de verificar. Esto significa que los problemas en P, también son problemas en NP, pero no todos los problemas en NP son problemas en P.

Por ejemplo, el problema de colorear un mapa con K colores de manera que no haya dos estados contiguos con el mismo color es un problema NP. Dados N estados y K colores, existen K^N maneras de colorearlo. Es decir que conforme el número de estados crece, el tiempo que tomaría encontrar una combinación válida aumenta exponencialmente. Sin embargo, si recibimos el mapa ya coloreado, sería bastante rápido verificar que no hay dos estados con los mismos colores. Tiene sentido, ¿no? Otro ejemplo de un problema en NP es el verificar si una expresión de lógica proposicional es una contradicción o no.

La clase NP tiene varias características interesantes. Dentro de esta clase hay una serie de problemas llamados NP-Completos. Las características principales de los problemas NP-Completos, son (1) se ha demostrado matemáticamente que cualquier problema NP-Completo no puede ser resuelto más rápido que ningún otro problema en P o NP (aunque podría ser resuelto en tiempo equivalente). La otra característica (en lenguaje sencillo) es que todos ellos son prácticamente equivalentes* entre sí. Es decir que la solución de un problema NP puede ser utilizada para resolver cualquier otro problema NP. De esta manera, por ejemplo, es posible expresar los colores de un mapa como una expresión de lógica proposicional(link en inglés), y resolver ambos problemas “al mismo tiempo”.

Vale la pena mencionar que la primera característica fue demostrada por el Teorema de Cook-Levin, uno de los resultados más importantes de la ciencia de la computación!

Una cuestión importante de NP es que hasta ahora, nadie ha demostrado que los problemas NP-Completos sean imposibles de resolver en tiempo polinomial. De hecho, es factible que exista un algoritmo que pueda resolver el problema de satisfabilidad booleana en tiempo polinomial; es sólo que nadie lo ha inventado/encontrado.

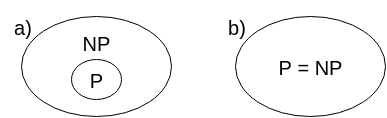
¿Se dan cuenta de lo que esto significa? Es decir que si alguien logra resolver uno solo de los problemas NP en tiempo polinomial, entonces todos los problemas NP en realidad son problemas P, y NP sería igual a P (NP = P). Y viceversa, si alguien demostrara que los problemas NP son imposibles de resolver en tiempo polinomial, entonces el mundo podría descansar y aceptar que los problemas NP-Completos en realidad no son fáciles de resolver. En la Figura 2 se ven los diagramas de Venn para cada uno de estos casos.

</img>
Figura 2. Los conjuntos P y NP. En (a), los conjuntos son diferentes (y los problemas en NP no pueden ser resueltos en tiempo polinomial). En (b) son iguales. Éste es uno de los problemas del milenio.

Por esto es que el problema de P vs NP es tan importante. Y por eso el resultado del profesor László Babai es tan interesante. Ahora vamos a hablar de Isomorfismo de Grafos.

Nota: El lenguaje que usé en esta sección es sencillo e impreciso a propósito; pero si quieren saber con más precisión de la Teoría de la Complejidad, y del problema de NP vs P, pueden estudiarlo en Wikipedia en español y en inglés, que es mucho más completo.

¿Qué descubrió Laci?

Ya que estudiamos la significancia de todo esto; entonces podemos ir al grano: la pregunta es si el problema de isomorfismo de grafos le pertenece a la clase P, o solamente a la clase de NP - y si no es P, sería NP-Completo? También podría no ser ninguno de los dos. Un problema que no es NP-Completo pero tampoco es P.

Aunque el profesor Lázsló aún no ha logrado mostrar que Isomorfismo de Grafos es un problema P, ha logrado mostrar que es muy cercano a P; contradiciendo lo que muchos suponían antes: que era cercano a NP-Completo. Esto lo hizo mostrando que el problema de Isomorfismo de Grafos es equivalente al problema de Isomorfismo de Cadenas, que es más general; y luego utilizando la técnica de Divide and Conquer para dividir el grafo en secciones más pequeñas que pueden ser resueltas recursivamente. El resultado es entonces:

Dados dos grafos, cada uno con N nodos, un algoritmo que determina si son isomórficos o no tiene un tiempo de ejcución de 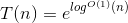. Esta función no es exactamente polinomial, así que se le llama cuasi-polinomial.

Este resultado es mejor que el mejor algoritmo que se conocía, cuyo tiempo de ejecución era 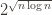. Como ven, este viejo algoritmo tiene un factor polinomial dentro del exponente, así que es un algoritmo cuasi-exponencial. Es decir que la diferencia es muy grande.

La prueba del resultado de Babai es larga, y difícil - y yo tampoco la entiendo bien. El borrador del artículo está disponible en ArXiV, y es prácticamente un libro: son 74 páginas de pruebas matemáticas y análisis. Laci también dio un seminario de tres sesiones donde explica su argumento, y está disponible en su sitio personal. Si les interesa este tema, pero el trabajo de Babai es muy avanzado, pueden empezar por Wikipedia, y luego este borrador del libro Computational Complexity: A modern approach escrito por dos profesores en la Universidad de Princeton son buenos recursos.

¿Y todo esto sirve para algo?

La cuestión de si dos grafos son isomórficos sí tiene aplicación fuera de la ciencia de la computación o las matemáticas. El estudio de grafos, o redes, ha crecido mucho en esta era en que la cantidad de información disponible ha crecido exponencialmente.

Una de las disciplinas que usan grafos continuamente es la Bioinformática, donde los nodos en un grafo pueden representar genes o proteínas y los vínculos entre ellos representan su nivel de coexpresión. De hecho, la teoría de grafos aplicada a la bioinformática ha sido utilizada para mejorar nuestra comprensión del cáncer en humanos, y en cómo diseñar curas.

Otro campo donde el isomorfismo de grafos podría ser útil sería en el análisis de redes sociales, y el estudio del internet.

Sin embargo, la mayor parte de las personas que estudian la teoría de la complejidad lo hacen por pura curiosidad matemática, no porque busquen implementar algoritmos más eficientes en las ciencias genómicas o de estudio de redes sociales ;). De hecho, los algoritmos sugeridos en todos estos artículos son puramente teóricos, y muchos no han sido implementados (aunque otros muchos sí lo han sido).

De cualquier forma espero que el post les pareciera interesante - ya sea que les gusten los algoritmos, o que les interese su aplicación. Hasta la próxima, y todos los comentarios son bienvenidos! ;)