En esta ocasión hablaremos de una estructura de datos muy interesante. Se trata de las Hash Tables (en español a veces se les conoce como tabla hash, matriz asociativa, mapa hash, tabla de dispersión o tabla fragmentada (1), en este post nos apegaremos a los nombres usados en inglés puesto que son más estándar y porque así podrán saber qué términos buscar si desean investigar más por su cuenta).

Una Hash Table es una estructura de datos que permite almacenar llaves (keys) y valores (values) y que puede usarse para implementar, por ejemplo, diccionarios.

Específicamente, en este post me gustaría platicarles sobre algunos conceptos fundamentales para entender cómo funcionan las Hash Tables y algunas de las dificultades que se presentan al tratar de implementar una buena función de hash. Esto nos permitirá sentar las bases que necesitaremos en post subsecuentes.

Tablas de Accesso Directo (Direct Addressing Tables)

Empecemos entonces con un ejemplo que nos sirva para motivar la implementación de una Hash Table. Imaginemos que tenemos el problema de representar el inventario de una fábrica. A nosotros se nos ocurre que podemos crear una estructura de datos que relacione, por ejemplo, la clave de cierto Item con su descripción. Quizás lo primero que se nos viene a la mente sea utilizar un arreglo. Algo más o menos así:

Item[0] = 'Tuerca grande'
Item[1] = 'Tuerca chica'
...
Item[98] = 'Tornillo chico'
Item[99] = 'Tornillo grande'

Una ventaja evidente de esta implementación es la capacidad de acceder fácilmente a una descripción a partir de la clave. Por ejemplo, si quisiéramos acceder al Item con clave 50, simplemente tendríamos que hacer Item(50). Muy fácil, ¿verdad?

Hash Tables y funciones de Hash

Bueno, podemos complicar el problema un poco si ahora decimos que las claves de los Items están en el rango de (0,19999), pero solamente existen 100 Items. La razón de que esto sea una complicación viene del hecho de que si quisiéramos directamente utilizar el método de crear un arreglo de 20K elementos, al final solamente estaríamos utilizando a lo más 100 de ellos. Podemos enseguida ver que esto sería un desperdicio de espacio.

En otras palabras, sería bastante conveniente poder mantener la capacidad de acceder fácilmente a cualquier descripción a partir de su clave, pero al mismo tiempo utilizar una cantidad razonable de memoria. Estas son dos de las propiedades que posee una Hash Table(3).

Una manera en que podríamos resolver esto sería, por ejemplo, acceder a la descripción del Item utilizando los últimos dos dígitos de la clave. Es decir, si queremos acceder al Item con clave 18789, entonces necesitamos buscar en Item(89).

Esta regla que acabamos de inventar para mapear una llave a una posición en el arreglo, es lo que conocemos como una función de hash. Para nuestro ejemplo, matemáticamente podríamos expresar nuestra función así:

h(key) = key % 100; // Produce valores entre 0 y 99

Como se puede observar, usando esta regla de conversión podemos seguir accediendo a nuestros elementos fácilmente y además seguimos utilizando una cantidad razonable de memoria para almacenar nuestros 100 Items.

La siguiente imagen nos ayudará a clarificar los conceptos de Key, Value, y Bucket (Slot).

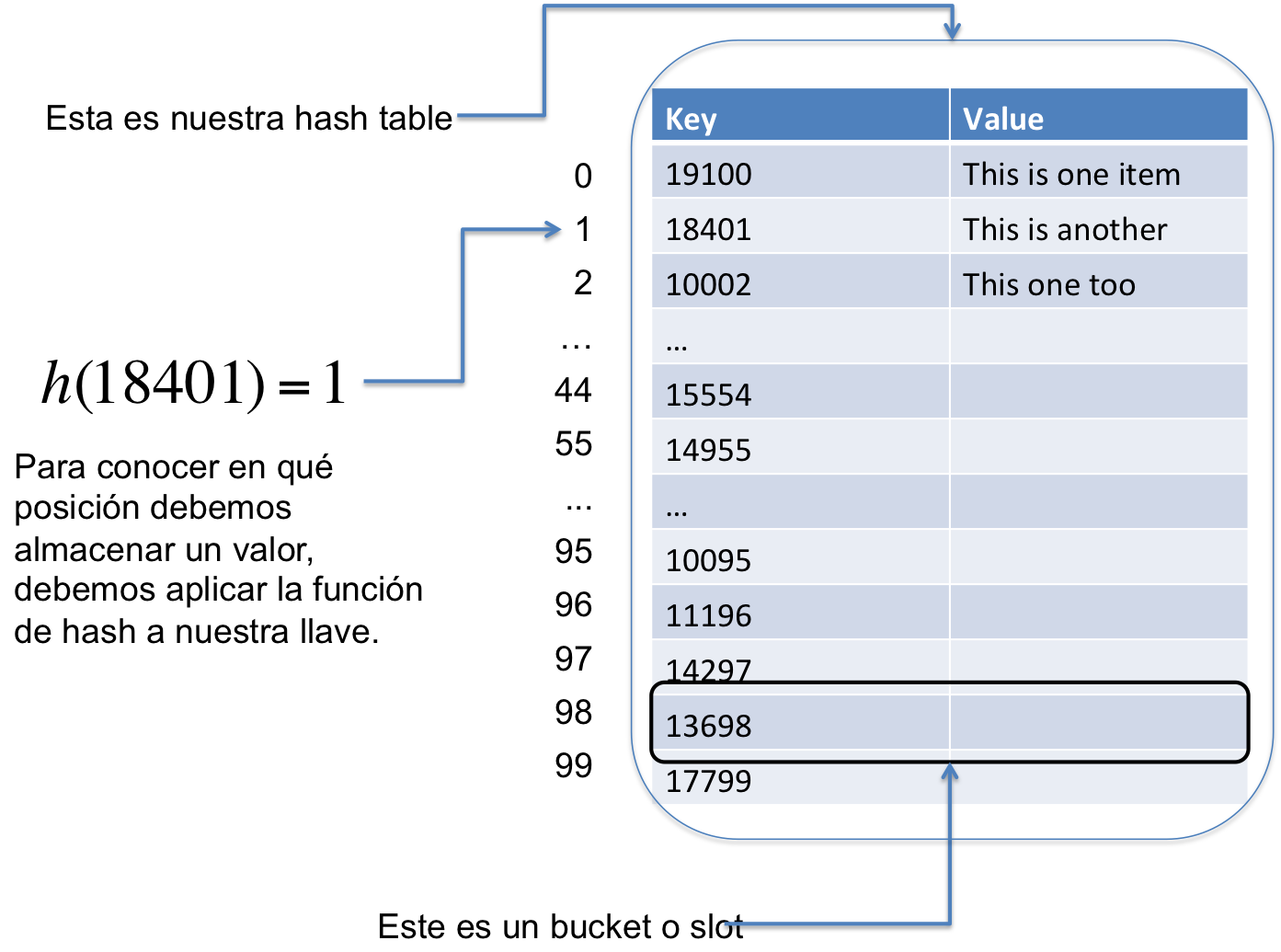
Con todos estos conceptos en mente, podemos entonces empezar a implementar una Hash Table. Una estructura Hash Table en C tiene más o menos la siguiente forma:

typedef struct HashTable {
  int num_elements;       /* Número de elementos que podemos almacenar */
  int buckets_vacios;     /* Número de buckets vacíos */
  int* keys;              /* Aca almacenamos las llaves */
  char** values;          /* Aca almacenamos los valores */
} HashTable_t;

Y el código para insertar un elemento tiene la siguiente forma básica. Con este código podemos empezar a ver un problema que vamos a encontrar con un Hash Table:

int insertar(HashTable_t *hashTableP, int key, char *value)
{
  int index;
  // Aplicar la función hash a la llave
  index = key % hashTableP->num_elements;

  // Si el bucket esta libre, insertamos nuestro valor ahi
  if (hashTableP->values[index] == NULL) {
    hashTableP->keys[index] = key;
    hashTableP->values[index] = strdup(value);
    hashTableP->buckets_vacios --;
  }

  // Si no esta libre, entonces tenemos una colisión.
  else {
    // ¿Y ora?
  }

  return 0;
}

Hash Collisions

Como ven, las dificultades no terminan aún ahí. Seguramente te habrás dado cuenta de que nuestra regla tiene un problema: es posible que dos o más llaves sean mapeadas a la misma posición en nuestro arreglo. Por ejemplo, 11001 y 11101 estarían utilizando la celda Item(1):

h(11001) = 11001 % 100 = 1 = 11101 % 100 = h(11101)

A esto se le llama “colisión” (Hash Collision). Una buena función de hash debe causar pocas colisiones, pero esto no es algo sencillo de conseguir. Una manera de esquivar este problema es usando técnicas de resolución de colisiones. Las dos técnicas más populares se conocen como “Separate Chaining” y “Open Addressing” (a ésta última algunos autores le llaman “Rehashing” (2)). Revisemos en esta ocasión la segunda técnica.

Open Addressing y Linear Probing

La estrategia de “Open Addressing” consiste en buscar algún otro bucket en el cuál colocar el elemento que deseamos insertar. En el ejemplo anterior podríamos por ejemplo elegir insertar nuestro elemento en Item(2) (porque Item(1) está ya ocupado). Si llegara a suceder que Item(2) también está ocupado, entonces podríamos intentar usar Item(3). En otras palabras se trata de encontrar el siguiente bucket disponible. A esta modalidad de “Open Addressing” se conoce como “Linear Probing”. La función de rehash puede escribirse así:

rh(i) = (i+1) % 100

Observemos que la entrada de la función ya no es la clave original, sino el índice generado al aplicar la función de hash original.

Ya hemos visto que aplicar la función de rehash una vez puede no ser suficiente para encontrar el siguiente bucket disponible. ¿Puedes imaginarte qué otros problemas puede haber con este método?

¿Qué pasaría si ya no hay ningún otro bucket disponible? Una implementación poco cuidadosa del rehashing podría ocasionar un ciclo infinito en nuestro código. Podemos resolver este problema teniendo alguna variable que nos indique si aún es posible encontrar un lugar vacío dentro de la Hash Table.

Aún si la tabla no estuviera llena, es posible caer en un ciclo infinito o en una situación en la que nuestra función de rehash nunca encuentre algún lugar disponible. ¿Puedes imaginar este caso? ¿Que pasaría por ejemplo con una función como rh(i) = (i+2) % 100? Sí, esta función intentaría únicamente utilizar posiciones pares o posiciones impares, dependiendo del valor de i.

Uno podría pensar que la única razón por la que esta función de rehash es mala es el hecho de que su rango no ocupe todas las posiciones posibles de la tabla. Las cosas podrían ser peor. Esta función de rehash puede mapear hasta a 50 posiciones. Usar una función como rh(i) = (i+20) % 100 es peor porque solo podríamos mapear hasta a 5 posiciones.

En pocas palabras, una propiedad deseable en una función de rehash es que para cualquier índice i, los posibles valores de salida cubran la mayor cantidad de posiciones posibles de la tabla. La función rh(i) = (i+1) % 100 en este sentido es una buena elección. Más generalmente, cualquier función rh(i) = (i+c) % table_size donde c y table_size son “primos relativos” (es decir, que no sean divisibles por un mismo numero diferente a 1) es una buena función (2).

Existen otros problemas muy interesantes en este tema de las Hash Tables. Fíjense que hasta ahora solo nos hemos enfocado en cómo resolver problemas a la hora de insertar nuevos elementos dentro de nuestra Hash Table. Las otras operaciones importantes son “buscar” y “borrar”… Pero por el momento dejémoslo hasta aquí para dejarles asimilar los conceptos que hemos revisado hasta ahora.

Les dejo el link a un gist para que vean una implementación sencilla de lo que aprendimos en esta ocasión: https://gist.github.com/rzavalet/7244952068a8c28ead89fbcd20bf0787.

Denle un vistazo al código para ver cómo funciona el rehashing, y para ejecutarlo pueden intentar lo siguiente:

$> git clone https://gist.github.com/rzavalet/7244952068a8c28ead89fbcd20bf0787 htable
$> cd htable
$> gcc hash.c
$> ./a.out

Y con eso van a poder ver cómo se ejecuta : )

Conclusiones

En este post hemos aprendido lo que es una Hash Table, una función de Hash, lo que son las Hash Collisions y una manera de resolverlas, llamada Open Addressing. Aprendimos que esta técnica también presenta problemas (bueno, en esta ocasión solo tocamos uno de ellos). En un post posterior aprenderemos otras maneras de resolver colisiones.

(1) https://es.wikipedia.org/wiki/Tabla_hash

(2) Langsam, Yedidyah et al. “Data structures using C and C++”. Prentice Hall, 1990.

(3) Cormen, Thomas et al. “Introduction to Algorithms”. MIT Press, 2009

Ricardo Zavaleta es un desarrollador Mexicano. De día hace distributed in-memory databases para Oracle, y de noche está completando su tesis para una maestría en sistemas y cómputo distribuído. Es fan de Pink Floyd y amante de Mario Benedetti.