Hablemos de PageRank
Recientemente, investigadores de la Universidad de Fribourg en Suiza han estado trabajando en un nuevo artículo donde estudian el profundamente el algoritmo de PageRank. Particularmente, este estudio se centra en el comportamiento de PageRank caundo es utilizado para analizar redes (también conocidas como grafos) que crecen con el tiempo. El artículo fue mencionado en la lista ‘Emerging Technology from the ArXiv’, de MIT Technology Review: Una lista semanal donde se seleccionan artículos novedosos e interesantes. Acabo de leer el artículo (en parte porque tengo que presentarlo en la escuela:P) y decidí escribir un pequeño post al respecto, dado que PageRank es un algoritmo famoso e importante.
¿Qué es PageRank?
Pues primero lo primero. Algunos tal vez nunca hayan escuchado el nombre, y algunos otros tal vez lo habrán escuchado pero no aprendieron los detalles de qué es y cómo funciona el algoritmo de PageRank. Para esas personas, vamos a revisarlo - y si tú ya conoces el algoritmo, puedes saltarte esta sección y leer ¿Qué dice el tal artículo?
El algoritmo PageRank fue desarrollado en 1996 en la Universidad de Stanford por Larry Page y Sergey Brin. ¿Les suenan? Éstos son los fundadores de Google, y PageRank fue el algoritmo que utilizaron para ordenar resultados web en las búsquedas de Google. Por cierto, [el artículo original donde Larry y Sergey presentan la anatomía de Google] (http://infolab.stanford.edu/pub/papers/google.pdf) está disponible en línea, y vale la pena checarlo.
De vuelta a PageRank. El algoritmo se basa en la idea de que sitios web importantes tienen muchas ligas que apuntan hacia ellos. Es decir, que si mi sitio web es importante, otros sitios web van a agregar ligas hacia él. Estas ideas sobre la importancia de los sitios web sugieren que la Web puede ser entendida como una red (valga la redundancia) de sitios que son conectados con ligas. La siguiente figura muestra una red con cuatro nodos, que podría representar cuatro sitios web que tienen ligas entre ellos.

Figura 1. Una red o grafo simple con cuatro nodos.
¿Porqué fue importante?
PageRank no fue el primer algoritmo en explorar la categorización de nodos en redes con base en su importancia. Sin embargo, Google fue de los primeros buscadores en utilizar un algoritmo de este tipo en su sistema de búsqueda. Hasta antes de eso, los buscadores utilizaban conteo de palabras clave para decidir qué sitios web son los más relevantes para una busqueda; es decir que si una persona busca “Pokemón”, los resultados serían sitios web con la palabra “Pokemón” escrita muchas veces. Esta métrica para ordenar los sitios web es bastante mala, dado que un sitio de baja calidad puede estar lleno de la palabra “Pokemón”, y parecer relevante; pero no tener ninguna información relevante o interesante más allá de la palabra “Pokemón”. Este sitio sería un resultado inútil.
Entonces, PageRank (junto con decisiones de negocio inteligentes) fue la chispa que convirtió a Google en una de las empresas más importantes del mundo. Es, de hecho, un algoritmo muy inteligente, que incluye muchos conceptos de probabilidad y ciencia de la computación. Vamos a echarnos el clavado a PageRank.
Detalles técnicos
Ahora vamos a explorar exactamente cómo funciona PageRank. PageRank es un algoritmo que recibe como entrada [un grafo]
(https://es.wikipedia.org/wiki/Grafo), que es una entidad matemática representada por un conjunto de nodos y un conjunto
de ligas entre esos nodos. En el ejemplo en la Figura 1, el conjunto de nodos es [1,2,3,4], y la lista de ligas
puede ser una lista de pares de nodos que están conectados, por ejemplo: [(1,2),(1,3),(3,2),(3,4),(4,3)]. Para leer más
sobre grafos, puedes checar el artículo de Wikipedia al respecto.
Entonces, PageRank recibe un grafo y calcula una distribución de probabilidad. Esta distribución representa la probabilidad de que si uno navega los links del grafo aleatoriamente, vaya a dar a un sitio web específico. En probabilidad existen varios problemas donde podemos imaginar a un ‘navegante’ que se mueve aleatoriamente en un espacio. Estos problemas son conocidos como caminos aleatorios. PageRank es un problema de este tipo, ya que supone que uno navega la web aleatoriamente a través de ligas. PageRank supone un camino aleatorio a través de la web.
Podemos considerar nuestro grafo de la Figura 1 como ejemplo. Imaginemos que cada uno de los nodos representa un sitio web,
y las conexiones entre ellos representan ligas. Si empezamos nuestro camino aleatorio en el nodo 1, tenemos
la misma probabilidad de que nuestro primer paso sea al nodo 2 o al nodo 3 - esta probabilidad es de 0.5, o de 50%.
Luego, para nuestro segundo paso, del nodo 3 podemos movernos a los nodos 2, o 4, cada uno con probabilidad 0.5;
mientras que el nodo 2 no tiene ninguna liga hacia otros nodos, así que ahí permanecemos en él con probabilidad igual a 1.
Vamos a sacar números para nuestros primeros dos pasos en la caminata aleatoria que parte del nodo número 1:
- Del nodo 1 podemos ir al nodo 2 con probabilidad 0.5. Luego:
- En el nodo 2 permanecemos con probabilidad 1.
- Del nodo 1 también podemos ir al nodo 3 con probabilidad 0.5. Luego, del nodo 3:
- Podemos ir al nodo 2 con probabilidad 0.5
- Podemos ir al nodo 4 con probabilidad 0.5
Estas decisiones pueden expresarse como un árbol de decisión con probabilidades que empieza en el nodo número 1, y camina aleatoriamente por el grafo. Se puede ver que tras dos pasos, la probabilidad de estar en el nodo número 2 es de 0.75, mientras que la probabilidad de estar en el nodo número 4 es de 0.25 (o 75% y 25% respectivamente). Noten que en este caso, la probabilidad de estar en cualqueir otro nodo es de cero.
 </img>
</img>
Figura 2. Árbol de probabilidades en una caminata aleatoria.
Pero esto sólo es el principio. PageRank considera una caminata aleatoria infinita. Si observamos la Figura 1, podemos ver que conforme la caminata aleatoria se vuelve más larga, la probabilidad de estar en el nodo número 2 tiende a 1 y la probabilidad de estar en cualquier otro nodo tiende a 0 (tómense un minuto para ir a la Figura 1 y verificar que es verdad). Esto no es ideal, así que PageRank tiene una condición extra: Un parámetro α, conocido como el ‘factor de amortiguamiento’. Cada turno, con probabilidad α volvemos a empezar la caminata, seleccionando cualquiera de los nodos aleatoriamente; y con probabilidad α-1 continuamos la caminata normalmente. Típicamente α tiene un valor de 0.15. De esta manera, la probabilidad de volver al nodo 1 se vuelve de 0.15 dividido entre los cuatro nodos.
Con la adición del parámetro α, PageRank tiene una distribución más uniforme, y no beneficia a algunos nodos desproporcionadamente. Ahora sí tenemos todos los ingredientes necesarios para un modelo completo. Agárrense, porque vamos a ir un poco rápido.
Existe un proceso estocástico (o proceso probabilístico) que permite modelar perfectamente esta clase de camino aleatorio. Es bastante famoso: La cadena de Márkov. Márkov era un matemático Ruso, que hizo varias contribuciones a la teoría de probabilidad. Platicaremos de él después. La cadena de Márkov es un proceso estocástico con un sinnúmero de aplicaciones prácticas; y que puede ser representado en forma de una matriz, donde se definen las probailidades de moverse de un nodo al otro en un camino aleatorio. Bajo esta idea, la matriz definida por el grafo de la Figura 1 (sin factor de amortiguamento) se ve así:
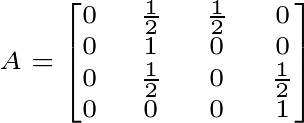 </img>
</img>
Figura 3. Matriz del Proceso de Markov para la caminata aleatoria en el grafo de la Figura 1.
Como ven, en la matriz A están las probabilidades de moverse de un nodo a otro. La probabilidad de moverse del nodo 1 al nodo 2 es 0.5, así que A[1,2] es 0.5. Lo mismo para el resto de la matriz.
Con cadenas de Markov existe un concepto conocido como la ‘distribución estacionaria’, donde dado un vector p, que
representa posiciones iniciales en el grafo, representa la probabilidad de estar en cada nodo al largo
plazo (¿les suena? Justo como PageRank); es decir:
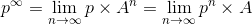 </img>
</img>
Figura 4. Ecuación de la distribución estacionaria.
Como ya habíamos mencionado, cuando no hay factor de amortiguamiento, todas las caminatas aleatorias terminan en el
nodo 2. Les dejo de tarea verificar que el vector p que resuelve la ecuación para la matriz de la figura 3 es el
vector [0,1,0,0]. (Nota: Para eso pueden usar www.wolframalpha.com!).
Y entonces, si agregamos el factor de amortiguamiento, la matriz que resulta es la siguiente:
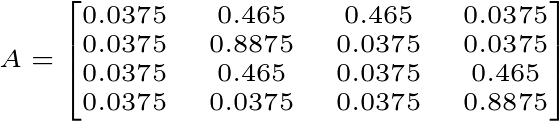 </img>
</img>
Figura 5. Matriz completa de pagerank para el grafo de la Figura 1.
¿De dónde salieron tantos decimales? Estos decimales resultan de agregar el factor de amortiguamiento de 0.15. Recordemos que 0.15/4 es 0.0375. Entonces, si estoy en el nodo 2, en vez de parmanecer ahí con probabilidad 1, voy a reiniciar el camino en un nodo aleatorio con probabilidad 0.15. Es decir que tengo probabilidad de 0.0375 de saltar a los nodos 1,3 o 4 y tengo probabilidad de 0.85 de permanacer en el nodo 2, más 0.0375 de ‘saltar’ al nodo 2 de nuevo: O sea 0.8875. El resto de las probabilidades puede calcularse de igual manera.
Ya no es tan fácil, pero tampoco es difícil resolver la ecuación de la Figura 4 utilizando la matriz de la Figura 5
- si utilizamos una herramienta como Matlab, Maple, o WolframAlpha ;). El resultado, tras algunas iteraciones,
es el vector
[0.0375,0.734,0.134,0.09]. Este vector es una distribución de probabilidad conocida como la distribución estacionaria de nuestro Modelo de Markov. Representa también la calificación de PageRank de cada uno de los nodos en nuestro grafo (Nodo 1: 0.0375; Nodo 2: 0.734; Nodo 3: 0.134; Nodo 4: 0.09). Esto nos permite rankear sitios web según su importancia! Es decir que el nodo 2 es el más importante, y después son el nodo 3, 4 y 1 respectivamente.
¿Qué tal?
Ahora que ya hemos hecho un ejemplo de PageRank, y tenemos una idea de qué es; podemos hablar del artículo donde fue PageRank fue analizado. Por cierto, para aquellos que quieren saber más de PageRank, hay una infinidad de recursos en línea, empezando por el artículo de Wikipedia en Español, el artículo de Wikipedia en inglés, que es mucho más completo y este sitio web de la Universidad de Cornell con muchos ejemplos.
¿Qué dice el tal artículo?
Suficientes bases de PageRank. Ahora toca hablar de lo que dice el famoso artículo hecho en Suiza. ¿Qué dice? Pues Mariani, Medo y Zhang observan que PageRank es un algoritmo muy popular. Es utilizado ampliamente en un sinnúmero de aplicaciones; por ejemplo el algoritmo de Google para rankear sitios web, ranking de [Artículos de investigación] (http://www.sciencedirect.com/science/article/pii/S0306457307001203) (siento esto está muy meta), e incluso estudiar las redes de interacciones entre proteínas en nuestras células. Los autores observan que PageRank es como un martillo que utilizamos para resolver todos nuestros problemas; pero que no todos los problemas son clavos. Es decir, que somos demasiado aventados a la hora de utilizar PageRank. Por eso este artículo es para estudiar en qué casos PageRank es una buena idea, y en qué casos no lo es tanto. Particularmente, se enfocan en los casos donde la red está en crecimiento constante, ya que sienten que estos casos no han sido bien estudiados. Un ejemplo son las redes sociales como Facebook y Twitter que crecen rápidamente: nuevos nodos y nuevas amistades aparecen todo el tiempo; otro ejemplo de red que crece con el tiempo son las redes de artículos científicos, donde artículos nuevos aparecen continuamente, pero no agregan nuevas referencias a otros artículos una vez que han sido publicados.
¿Cómo le hicieron?
Los autores estudian el comportamiento de PageRank de dos maneras: Con una [simulación Monte Carlo] (https://es.wikipedia.org/wiki/M%C3%A9todo_de_Montecarlo), y con dos bases de datos con información real. Las bases de información real fueron una red social (la de Digg.com) y una red de artículos científicos (de American Physical Society). Los resultados de sus experimentos contribuyeron a la hipótesis de que existen casos donde PageRank no es una elección ideal en ciertos casos.
Simulaciones de Montecarlo
Una simulación de Montecarlo no es más que la simulación de un proceso utilizando datos generados por computadora. Es un campo de estudio fascinante, y es un método muy común en el estudio de grafos. Para este artículo, los datos consistieron en grafos generados aleatoriamente, pero con ciertas reglas. Para ser concisos, basta con decir que los investigadores utilizaron una estrategia llamada Modelo Barabási-Albert, que permite generar grafos aleatorios que se parecen mucho a los grafos que se obtienen en el mundo real, tal como las redes sociales.
La idea del Modelo Barabási-Albert es que unos pocos nodos son muy populares, mientras que el resto son “promedio”. Éste es un fenómeno fácil de ver en Facebook: El usuario promedio tiene menos de 300 amigos, pero existen algunos usuarios que tienen varios cientos, y varios miles de amigos. Este tipo de redes tienen la característica que los nodos más populares se vuelven aún más populares, y los demás permanecen en el promedio. Algo así como el fenómeno de dinero llama dinero.
De vuelta al artículo, los autores encontraron en sus simulaciones que PageRank depende de dos parámetros muy importantes para ser preciso: La actividad de un nodo, y la relevancia de un nodo. ¿Qué son éstos?
- La actividad de un nodo mide qué tan activo es el nodo para agregar nuevas conexiones. Si un nodo se conecta a nuevos nodos cada turno, es un nodo activo; mientras que si un nodo no está haciendo conexiones nuevas, es un nodo inactivo.
- La relevancia de un nodo es una medida de su habilidad para atraer conexiones. Si soy muy divertido, aunque tenga pocos amigos, tengo la habildiad de atraer muchos amigos nuevos. Los autores asumen que PageRank debe poder descubrir esta clase de nodos.
Los autores modelan la actividad y la relevancia como cantidades que decrecen con el tiempo. Un artículo científico se vuelve menos relevante con el tiempo; y una persona en Facebook agrega a la mayoría de sus amigos al principio, y después agrega menos conforme el tiempo pasa. Parece razonable.
Los resultados en las simulaciones fueron que PageRank funciona bien en redes donde la actividad y la relevancia decaen a velocidades similares. Las redes sociales son un buen ejemplo: Un usuario en Twitter que pasa mucho tiempo en Twitter puede publicar contenido interesante, y buscar nuevos usuarios que seguir: mientras que un usuario que no usa Twitter mucho es poco relevante y poco activo. PageRank es un buen algoritmo para rankear elementos de una red social por importancia.
Por otro lado, los autores mencionan que en redes donde la actividad y la relevancia decrecen a velocidades muy diferentes, PageRank es bastante malo para reconocer los nodos más relevantes. Las redes de Artículos Científicos son un buen ejemplo. Un artículo puede ser relevante por mucho tiempo, pero una vez que es publicado, no vuelve a citar a ningún otro artículo. Es decir que la relevancia decae lentamente, mientras que la actividad decae inmediatamente; y esto provoca que PageRank sea sesgado hacia nodos viejos.
En el caso contrario, en pruebas donde la actividad decae lentamente, y la relevancia decae inmediatamente, los autores encontraron que PageRank tiene un serio sesgo que favorece nodos nuevos. Puntos extra para la persona que tenga una idea sobre una red que muestre actividad de largo plazo y relevancia de corto plazo : ).
Resultados en datos reales
Las simulaciones dieron el resultado esperado, pero es importante verificar esta clase de hipótesis con datos reales. Cuando los autores del artículo decidieron aplicar su metodología a datos reales se encontraron con un problema en particular: Estimar la relevancia de un artículo científico, o de un usuario en una red social. ¿Cómo hacerle? Ése es el problema que PageRank trata de resolver, así que ellos tenían que encontrar una manera alternativa de calcular la relevancia de un nodo (y por cierto, en mi opinión ésta es una debilidad importante de este artículo).
Bajo el esquema que los autores diseñaron, encontraron lo esperado: La red de la American Physical Society, una red de artículos científicos mostró que PageRank tiende a favorecer nodos antiguos; y que el número de citas es una medida mucho más precisa de la importancia de un artículo.
Para los datos de Digg.com, donde los nodos representan usuarios y las conexiones representan ‘follows’, o seguidores, dado que la red social tiene un comportamiento de relevancia y actividad similar, PageRank resultó ser una buena medida de la importancia de un nodo; pero la cuenta de seguidores de un usuario de nuevo fue un indicador más útil.
Discusión y conclusiones
Pues bueno, así es esto. El artículo es bastante completo, y de hecho los autores realizaron muchos experimentos detallados. Sin duda, el artículo tiene una debilidad: Los autores están tratando de medir el desempeño de PageRank. PageRank es una herramienta que trata de estimar la importancia de un nodo en un grafo; sin embargo, la importancia de un nodo en un grafo de datos reales es muy difícil de estimar. ¿Cómo saber si un Twittero es el más importante? ¿O un artículo científico? Pues en este artículo, diseñaron una medida que pretende ser mejor que PageRank, pero ¿quién sabe?
De cualquier forma, el artículo es inteligente, y presenta un buen punto: Hay que tener cuidado con las herramientas que utilizamos para resolver nuestros problemas. No todos los problemas son clavos, y el martillo no es la única herramienta. PageRank es un algoritmo brillante, interesante y útil; pero hay que detenernos a pensar antes de aplicarlo a nuestros datos o realizar una aplicación que depanda de PageRank.
